
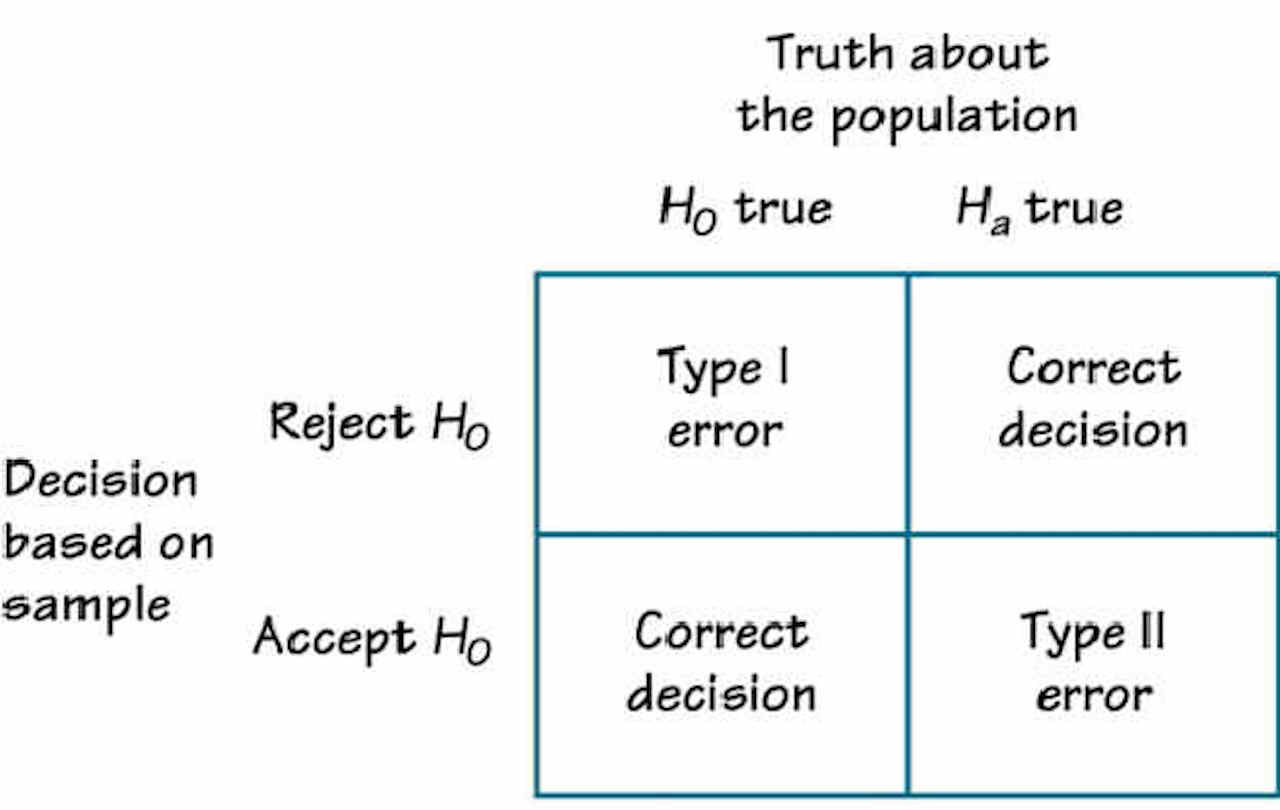

4-to-.6 interval then you’ll judge the coin to be fair, and if the number of heads is outside the. You’re going to use the 95% interval to make your judgment: If the number of heads is within the. Your task is to test two arbitrary coins by flipping each one 100 times. The basket has an unknown number of fair coins and an unknown number of unfair coins. Imagine that I present you with a basket full of coins. Let’s explore these two types of potential errors with some examples. What about unfair coins that mislead us and lie inside the interval? That will lead us to erroneously declare them fair. Only 5% of the time will a fair coin mislead us and lie outside the interval, leading us to erroneously declare it unfair. Any coin whose proportion of heads lies outside the interval we’ll declare unfair. 6 boundary lines to make a 95% confidence interval for testing coins.
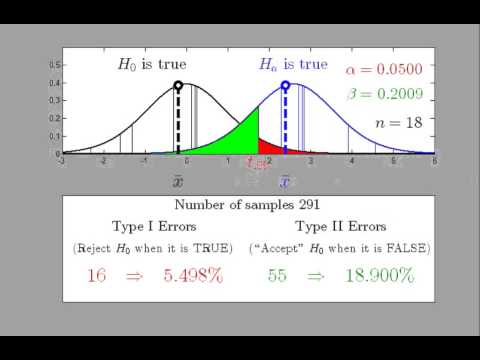
We’ll start off using a sample size of 100 and.


 0 kommentar(er)
0 kommentar(er)
